Como ler e escrever números muito grandes ou muito pequenos

Os números muito grandes ou muito pequenos podem ser representados por potências de base 10

Para o uso comum no dia a dia, até a casa do bilhão ou trilhão parece ser suficiente para a comunicação fluir naturalmente na sociedade. Mas existem objetos "astronômicos" ou "microscópicos" que precisam ser medidos. Daí, a necessidade dos números que expressam coisas muito grandes ou muito pequenas. 

Os números inteiros podem ser aumentados infinitamente, acrescentando algarismos. E os números decimais, que se situam entre 1 e zero, podem ser reduzidos indefinidamente, aumentando as casas decimais.

Os números podem ficar "muito grandes" ou "muito pequenos", como na figura abaixo: 

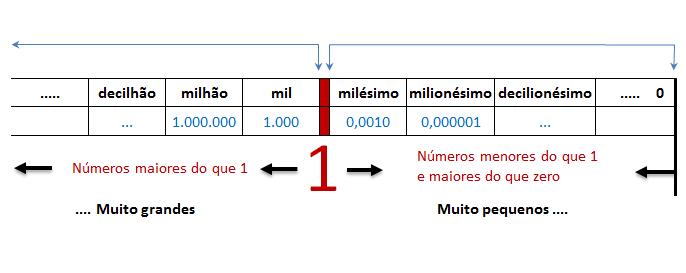
A figura mostra que os números acima de 1 podem crescer indefinidamente, formando números muito grandes. Por outro lado, os números menores do que 1, à medida que vai diminuindo, tendem a zero. O número zero significa que nada existe, mas os números decimais podem ser reduzidos indefinidamente aumentando as casas decimais com acréscimo de zeros logo após a vírgula.

Entretanto, os números muito grandes, como quintilhão e decilhão, ou muito pequenos, como quintilionésimo e decilionésimo, fogem à nossa imaginação. Quanto valem esses números? São comparáveis com quê? Esses números são utilizados nos diversos campos da Ciência (Engenharia, Química, Física, Biologia, Matemática etc.).

1. Leitura e grafia de números muito grandes

Listamos na tabela abaixo os numerais cardinais a partir de mil, bem como a forma de leitura e representação em notação científica ou exponencial (potência de base 10). A quantidade de zeros de cada numeral é igual ao número de potência da base decimal. Por exemplo, a classe de trilhão tem 9 zeros e a de sextilhão tem 21 zeros após o algarismo 1.

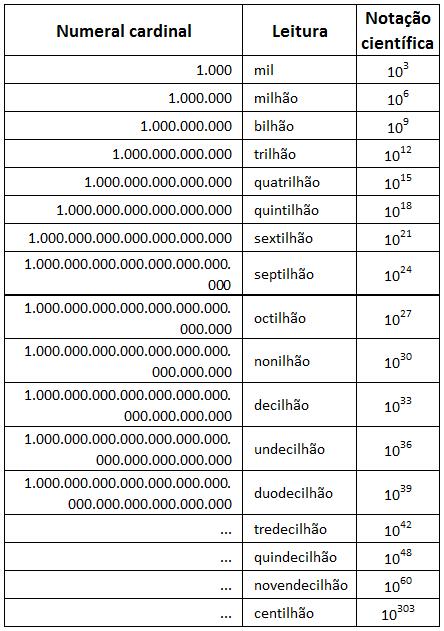
A potência de base 10 significa que o número 10 é multiplicado por ele mesmo X vezes. Por exemplo, potência 9 na base 10 representa um bilhão. É como se o número 10 fosse multiplicado 9 vezes, como segue: 

1 bilhão = 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10  = 1.000.000.000.

Para ler ou escrever números cardinais, é só seguir a ordem da tabela acima.

Exemplos:

1.000 = mil

21.000 = vinte e um mil

321.000 = trezentos e vinte e um mil

4.321.000 = quatro milhões, trezentos e vinte e um mil

54.321.000 = cinquenta e quatro milhões, trezentos e vinte e um mil

654.321.000 = seiscentos e cinquenta e quatro milhões, trezentos e vinte e um mil

7.654.321.000 = sete bilhões, seiscentos e cinquenta e quatro milhões, trezentos e vinte e um mil

E assim por diante.

Por questões de funcionalidade, para expressar um número muito grande, é comum arredondá-lo e escrever por extenso. 

Exemplos:

O corpo humano é formado por 10 trilhões de células e 7 octilhões de átomos (7 seguido de 27 zeros).

A estrela mais próxima de nós, a Proxima Centauri, está a 4,3 anos-luz de distância, ou seja, a 40,8 trilhões de quilômetros (40,8 seguidos de 11 zeros) ou, arredondando o número, 41 trilhões de quilômetros (41 seguidos de 12 zeros).  

NOTA: 40,8 trilhões é representado pelo número 40.800.000.000.000 e 41 trilhões, pelo número 41.000.000.000.000. O algarismo 8, que vem logo após a vírgula no número 40,8 trilhões, está no lugar do primeiro dos 12 zeros utilizados para expressar 41 trilhões.

2. Leitura e grafia de números muito pequenos

Números decimais muito pequenos (pequenos em valor), como sextilionésimo ou decilionésimo não são comuns no dia a dia. Mas esses números são usados em ciências (Física, Engenharia, Biologia etc.).

Quando o número decimal é muito pequeno (quanto maior a potência negativa, menor é o número), costuma-se expressá-lo também em notação científica (potência de base 10). Por exemplo, 25 septilionésimos pode ser representado por 25 elevado à potência "negativa" de 24 (25^-24), o que significa que existem 24 casas decimais no número.

A tabela seguinte mostra os numerais ordinais em algarismo e como podem ser lidos, bem como a forma de representação matemática com potência de base 10. Por exemplo, em vez de escrever 32 trilionésimos na forma decimal 0,000000000032, seria mais fácil e menos sujeito a erro escrevê-lo na forma de potência, ou seja, 32 elevado à potência negativa de 12, facilitando também a leitura.

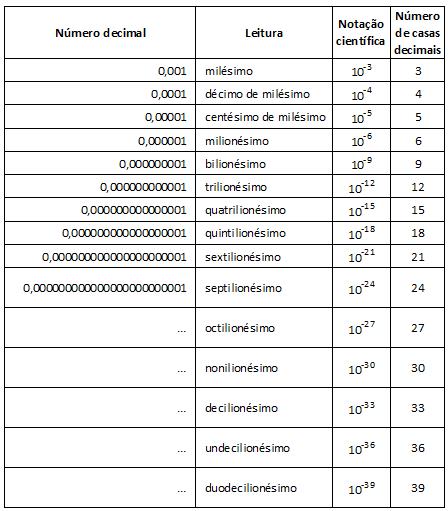
    NOTA:  Leitura de acordo com VOLP (Vocabulário Ortográfico da Língua Portuguesa da Academia Brasileira de Letras). 

Exemplos:

1 nanômetro corresponde a 1 metro x 10 na potência negativa de 9 (1 x 10^-9), ou seja, 0,000000001 metro (9 casas decimais).

Existem bactérias que medem 1 micrômetro (1^-6 metro), ou seja, 0,000001 metro (6 casas decimais).

Células de seres vivos podem chegar a medir 50 micrômetros (50^-6 metro), ou seja, 0,000050 metro (6 casas decimais).

Os números decimais podem ser representados com potências de números negativos e podem ser convertidos também em forma fracionária.

Exemplos: 

Adicionar comentário